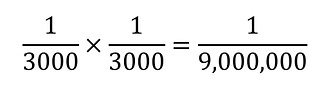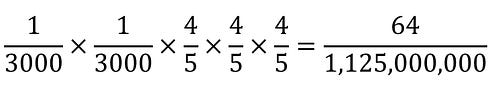Jordan Peterson's calculation of the probability of having both a transexual and pansexual child

Upfront disclaimer: most of the numbers in what follows are either unknown with any real degree of accuracy or will have changed significantly since there were any real data to substantiate them. Also, while we show Peterson’s calculations are wrong, we are strongly sympathetic to the main point he is making.

Background

In March 2022 Disney corporate president Karey Burke said, "as the mother [of] one transgender child and one pansexual child," she supports having "many, many, many LGBTQIA characters in our stories" and wants a minimum of 50 percent of characters to be LGBTQIA and racial minorities.

For those of you who are unaware of the definitions of the multitude of LGBTQ+ categories:

• A transsexual individual identifies as a gender different from their assigned sex at birth

• A pansexual individual is sexually attracted to others regardless of their gender identity or biological sex.

In a recent podcast with Joe Rogan, Jordan Peterson commented on that saying

"The joint probability that you have a trans kid and a pansexual kid is one in nine million." "The odds that you're a pathological narcissist sacrificing your own children to the glorification of your compassion is eight million, nine hundred and ninety-nine thousand, nine hundred and ninety-nine to one."

Peterson’s calculation

Peterson makes two probability calculations:

1. The probability of having one transexual child and one pansexual child

2. The probability the mother of such children (one transexual the other pansexual) is a pathological narcissist

It turns out that both are incorrect based on the assumptions he makes. We will leave the second probability until the end and focus first on the probability of having one transexual child and one pansexual child. As you can see from the video, Peterson bases his calculation of this probability on the following explicit assumptions:

• “The probability a child is transexual is 1 in 3000”

• “The probability a child is pansexual is even less than the probability of being transexual, but let’s assume it is also 1 in 3000”

His calculation of what he refers to as the ‘joint probability’ of having one transexual child and one pansexual child also assumes that these two events are independent of each other. If two events are independent of each other, then the probability of both events happening is equal to the product of the two probabilities, so in the case we get his result:

But, this is incorrect.

Error 1 (this is basic)

Even if we assume ‘independence’ there is a basic error here. It’s the same error people make when asked to calculate the probability that, in a family with two children, one is a boy and one is a girl. Assuming the probability of a boy is 1/2 and the probability of a girl is 1/2, then is it the case that the probability of one boy and one girl is 1/4?

NO!!!!!!!

That’s because in a family of 2 children there are 4 possible outcomes:

1. Child 1 is boy, Child 2 is a boy

2. Child 1 is boy, Child 2 is a girl

3. Child 1 is girl, Child 2 is a boy

4. Child 1 is girl, Child 2 is a girl

While it is true that each of these has a probability 1/4, there are TWO cases resulting in one boy and one girl. Hence, the probability that, in a family of 2 children there will be one boy and girl, is 1/2 not 1/4.

By exactly the same reasoning a family with one transexual child and one pansexual child can occur in two different ways:

1. Child 1 is transexual, Child 2 is pansexual

2. Child 1 is pansexual, Child 2 is transexual

By Peterson’s assumptions each of these has probability 1 in 9 million. But that means the probability of having one transexual child and one pansexual child is 1 in 4.5 million.

Error 2 (this is also basic)

The 1 in 4.5 million probability using Peterson’s assumptions only works if these were Karey Burke’s only children. But, in fact, she has FIVE children, and we can reasonably assume that none of the other three children come under any LGBQT+ category. This changes the probability significantly because the real probability we are asking is

Of Burke’s five children, what is the probability that one is transexual and one is pansexual?

This is a classical ‘Binomial theorem’ problem, but we can show the necessary calculations from first principles without having to resort to any formulas. We have to consider all possible outcomes for the 5 children; for example, one such outcome is:

Child 1 is transexual, Child 2 is pansexual, Children 3, 4 and 5 are not LGBTQ+

For simplicity we represent this as the sequence

T P X X X

where T is transexual, P pansexual, and X is not LGBTQ+

To calculate the probability of this exact sequence we need to know the probability of X. A common error would be to assume that this is the same as the probability as “neither transexual no pansexual’ but this is wrong because LGBTQ+ includes much more common categories, such as gays and lesbians. In fact, according to AI searches more than 20% of the current generation of children in the US identify as LGBTQ+. So, even if we remove the specific transexual and pansexual categories, then it is reasonable to assume the probability of X (a child not being in any LGBTQ+) category is about 80%, i.e. 4/5.

This means that the probability of the specific sequence T P X X X is

That is 1 in 17,578,125.

But there are 20 different possible sequences each with the same probability:

T P X X X

P T X X X

X T P X X

X P T X X

X X T P X

… etc

Hence, the probability is 20 in 17,578,125 which is 1 in 878,906, i.e. better than 1 in a million chance.

Error 3 (this is the most fundamental)

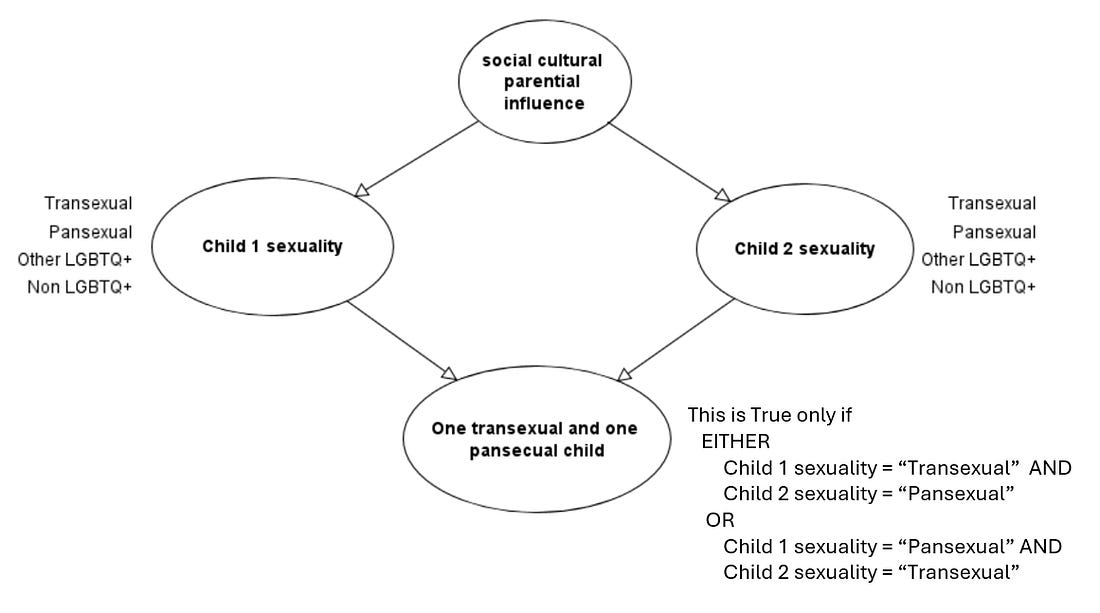
Although there is no evidence of any genetic link to LGBTQ+ identification among siblings, there are (as Peterson himself clearly implies) social/cultural/parenting influences that mean that siblings’ sexual identification are not independent. For example, it is known that LGBTQ+ identification is higher among children of Democrats than Republicans. Therefore, if we stick for simplicity to the case where there are only two children, the correct causal model is this one in which social/cultural/parenting influence (a common causal factor) creates an indirect dependency/correlation between the siblings sexual identification:

If the influences are present, then each child has a higher probability of being transexual/pansexual than if the influences are not present (there will also be a higher probability of the child being in the “Other LGBTQ+” category).

For simplicity, let’s assume that there either is or not social/cultural/parental influence over sexuality.

If there is such influence, let’s assume that instead of the 1 in 3000 (i.e. 0.000333) assumed by Peterson:

the probability of a transexual or pansexual child is 0.0005 (i.e in 1 in 2000)

If there is no such influence:

the probability of a transexual or pansexual child is 0.0001 (i.e. 1 in 10,000)

The full model including assumptions, along how these influence the prior probabilities are shown in the Appendix, which also explains all the results in what follows.

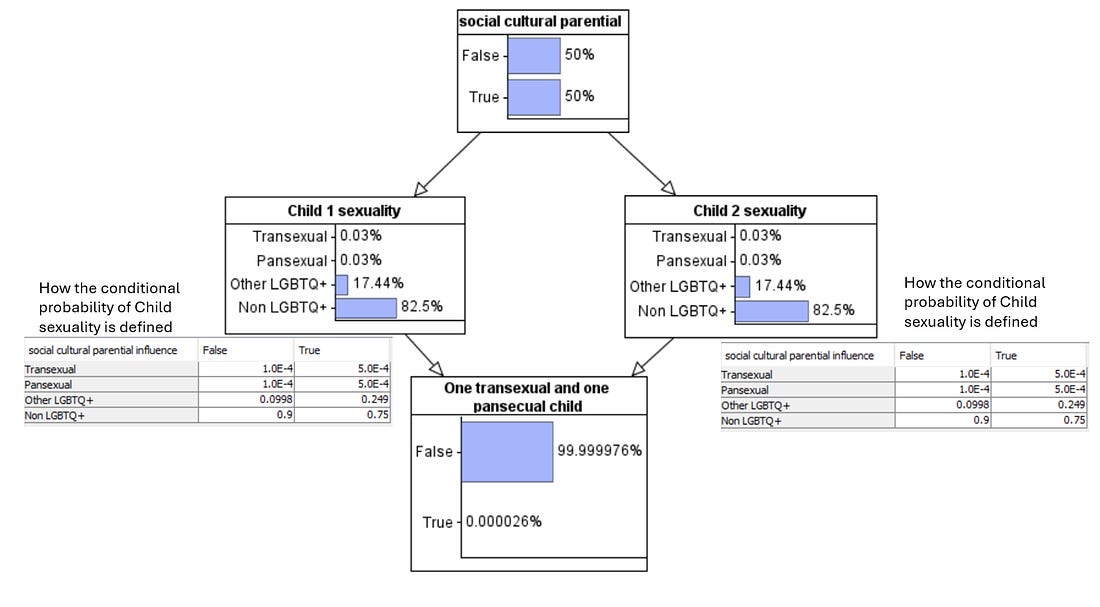
Note that, before we know anything about this family the (prior marginal) probability that one child is pansexual and the other transexual is 0.000026%, which is about 1 in 4 million¹.

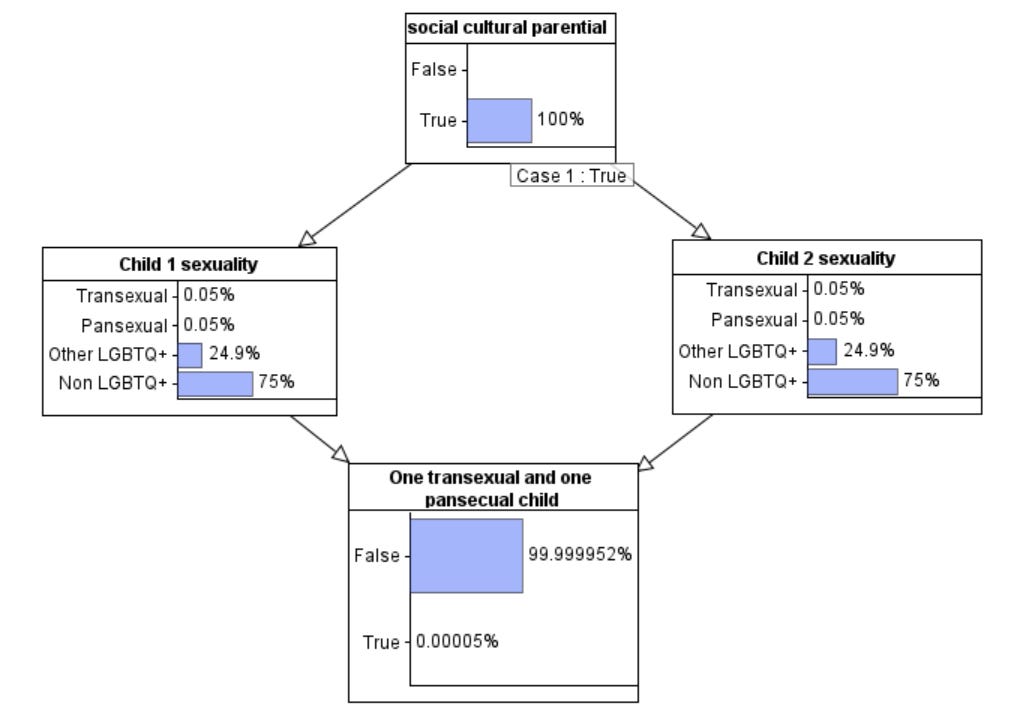
However, if we know there are social/cultural/parental influences then the probability that one child is pansexual and the other transexual increases to 0.00005%, which is about 1 in 2 million. So, the probability increases significantly, but it is still extremely unlikely. However, the interesting result is what happens when we observe that there is one pansexual and one transexual child, and it is this result that addresses the second probability that Jordan Peterson claimed. We consider this next.

What is the probability the mother of two children - one transexual the one pansexual - is a pathological narcissist?

Peterson claimed this probability was 8,999,999/9,000,000 (which is 99.99999888%). The basis for this claim is that this is 1 minus 1/9,000,000 (i.e. 1 minus the probability that the mother would have one transexual and one pansexual child).

Even ignoring the error in the 1/9,000,000 calculation, Peterson makes a classical probability fallacy error here (the fallacy of the transposed conditional, or “prosecutor’s fallacy”). He is assuming that

Probability of “not H” given E = Probability of E given “not H”

where H is the hypothesis “pathological narcissist mother” and E is “mother has one transexual and one pansexual child”

(we write this as P(not H | E) = P(E | not H))

Specifically, he assumes that P(E | not H) = 1/9,000,000 and, by the above fallacy, he assumes this means that P(not H | E) = 1/9,000,000. From that it would follow that

P(H | E) = 1 minus 1/9,000,000.

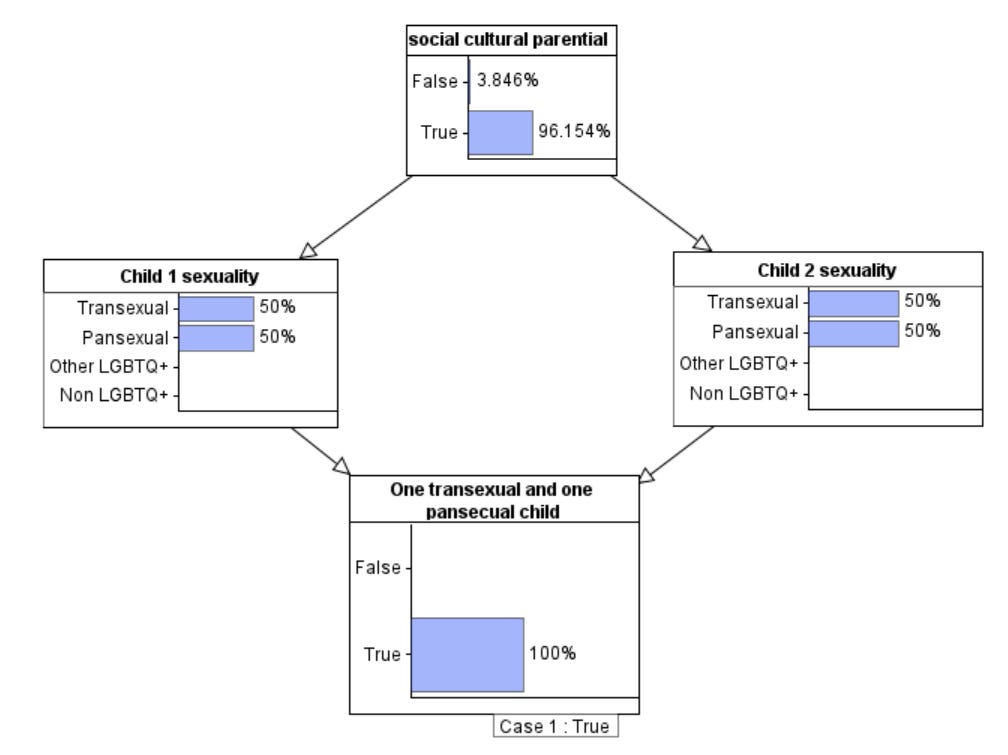
In fact, while the hypothesis “pathological narcissist mother” is rather ill-defined, it is reasonable to assume that this is a surrogate for the “social/cultural/parental influences” that we added to our causal model.

We can compute the probability that there are “social/cultural/parental influences” given the observations that one child is transexual and the other pansexual. Based on the prior assumption that this was 50%, the probability increases to over 96%. So, although this is less than Peterson’s estimate of 99.99999888%, it is indeed still very likely given the reasonable assumptions in the model.

Other possible errors/considerations

We have identified clear (but very common) probabilistic errors in Peterson’s calculations. His assumptions (which we have adopted) also ignore other factors that would significantly change the probabilities. These include the following:

• According to recent surveys children identifying as ‘pansexual’ is far more common than Peterson assumes. He said it was a term that “wasn’t even known about 5 years ago” and that, therefore, it was surely even less than the 1 in 3,000 probability of a transexual. But, according to AI searches, in the US between 1-2% of children between the ages of 14-18 now identify as pansexual.

• Peterson calculates the specific probability of one transexual and one pansexual child. But his argument would also have applied to other combinations like: two transexual, two pansexual, or indeed any of the other myriad of rare LGBTA+ categories. So, the actual probability we should be computing is:

what is the probability that two children identify as a relatively rare LGBTQ+ category like: transexual, pansexual, asexual, non-binary, omnisexual, abrosexual, demisexual, graysexual, autosexual, pomosexual, quoisexual/quoiromantic, androsexual/gynosexual, skoliosexual, aegosexual, …?

The resulting probability is significantly higher.

Conclusion

The fact that Disney corporate president Karey Burke is demanding at least 50% of Disney characters be LGBTQ+ and racial minorities suggests that she is highly committed to the agenda of encouraging ‘diversity’. It does, therefore, seem reasonable to conclude that these views may have had some influence on the fact that she has one transexual and one pansexual child. Jordan Peterson made some basic assumptions about the probability of a child being transexual or being pansexual and from these provided a basic calculation of how unlikely it was that Burke had one transexual and one pansexual child by chance alone, and hence how likely it was that the outcome was the result of Karey Burke’s influence.

We have shown that Peterson made some basic, but very common probabilistic errors in his calculation, even given his assumptions were correct. While I don’t believe there was ever a real intention by Peterson to claim that the figures were highly accurate, it is important to highlight and explain how to fix these errors because they are so common in all types of probabilistic and statistical reasoning.

Once the errors are fixed it turns out that Peterson’s calculations underestimate the probability (by chance alone) of the observed outcomes for Burke’s children, and overestimate the probability of her being a ‘pathological narcissist’ sacrificing her own children to the glorification of her compassion to diversity. Nevertheless, the corrected calculations demonstrate that there is still substance to the thrust of Peterson’s claims.

Appendix: The Bayesian network model